- To learn about the high-energy processes that release high energy (>500 MeV) protons at the Sun.
- To learn about the processes that affect their propagation in the interplanetary space up to the Earth orbit.
- In addition, the output of the GLE inversion software can be used to estimate the particle fluxes at 1 AU to assess e.g. radiation dose rates at flight altitudes.
Procedure to achieve the goals
The origin of solar particle events can be unfolded by solving the inverse problem of processing data that has been subject to mostly known blurring mechanisms (interplanetary transport and detection). The GLE inversion software attempts the first direct inversion of NM data to infer the solar source characteristics and the conditions under which relativistic solar energetic particles (SEPs) propagated in the interplanetary medium. One of the advantages of this approach is that the functionality of the pitch-angle distributions of the primary cosmic rays at 1 AU does not need to be fixed a priori, allowing different forms and variable shapes as a function of rigidity.
To formulate the problem with an inverse modeling approach it is necessary to be able to compute the response of the system to an impulsive (delta) injection of particles at the Sun, i.e. the Green's function. Convolution then allows us to determine the response to more complex inputs, e.g.
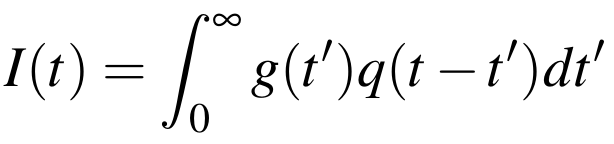
where I(t) is the sum of impulsive responses resulting from a series of releases at the Sun, g(t) is the system's Green's function, and q(t) is the input injection profile. For simplicity, here we assume that the response is only time-dependent, but the same holds if one includes the energetic and directional dependence in the Green's function.
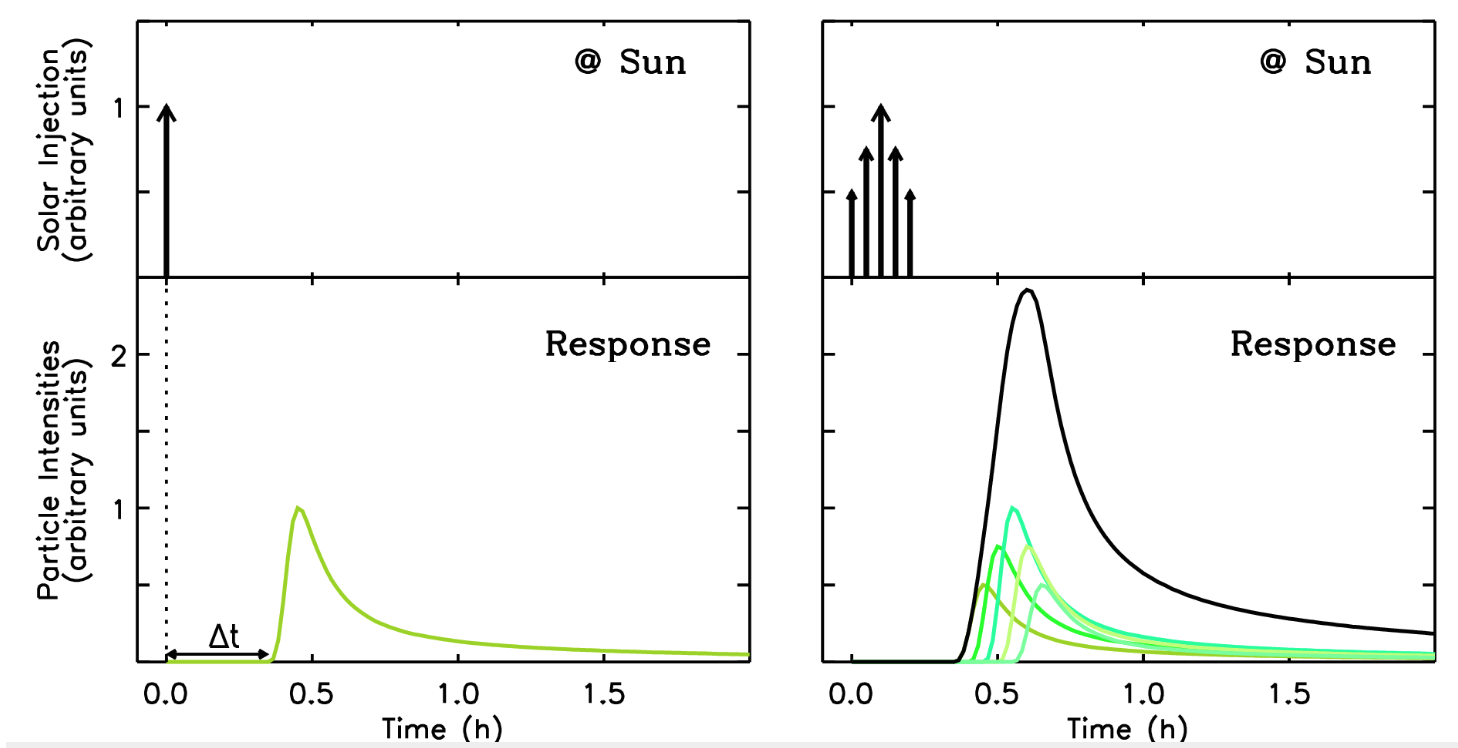
Let's consider an arbitrary function q(t) -to be determined- that represents the injection function of SEPs close to the Sun. The modeled intensities, M, can be written as a convolution of the Green's function with the injection function. The inversion problem requires to solve the following equation subject to the constraint that the injection profile can not be negative

where J are the observations and g is a matrix containing the impulsive response of the system for different release times at the Sun. We use the Non-Negative Least Squares (NNLS) method developed by Lawson & Hanson (1974).
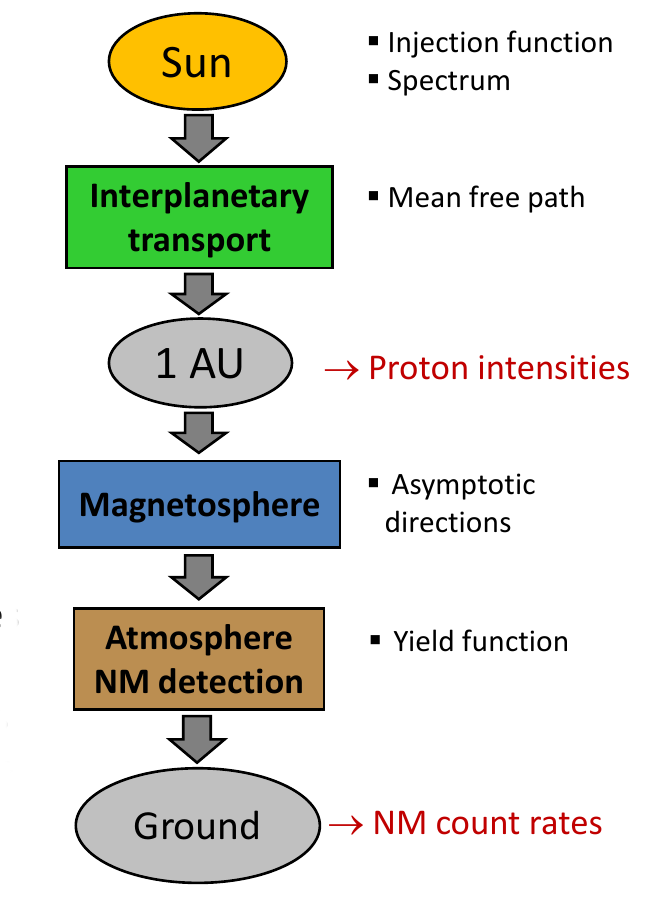
To compute the response expected at different times at different NM stations, the GLE inversion software uses several models, including the propagation of relativistic SEPs in the interplanetary space from the Sun to the Earth, the transport in the geomagnetosphere and in the Earth’s atmosphere, as well as the detection of the nucleon component of the secondary cosmic rays in the atmosphere by the NMs.

 hesperia [dot] info [at] hesperia-space [dot] eu
hesperia [dot] info [at] hesperia-space [dot] eu