SEP Injection at the Sun and Interplanetary Propagation to the Top of the Geomagnetosphere
In an unperturbed solar wind, the interplanetary magnetic field (IMF) can be described as a smooth average field, represented by an Archimedean spiral, with superposed magnetic fluctuations. In this case, the propagation of solar energetic particles (SEPs) along the IMF is affected by both the effects of adiabatic motion along the smooth field and pitch-angle scattering by magnetic turbulence.
The quantitative treatment of the evolution of the particle’s phase space density, f(z,μ,t), can be described by the focused transport equation (Roelof 1969):

Here z is the distance along the magnetic field line, μ = cos α, is the cosine of the particle pitch angle, α, and t is the time. The injection of particles close to the Sun is given by q(z, μ,t). The systematic force is characterized by the focusing length, L(z) = −B(z)/(∂B/∂z), in the diverging magnetic field B, while the stochastic forces are described by the pitch-angle diffusion coefficient Dμμ(μ). Under strong scattering conditions, the parallel scattering mean free path, λ||, is related to Dμμ by (Hasselman & Wibberenz)
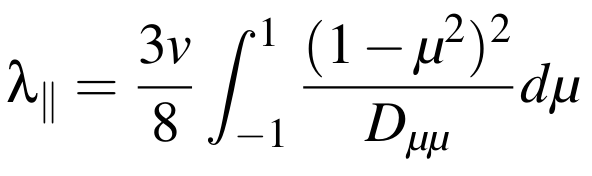
The mean free path has proved to be a convenient parameter to characterize the amount of scattering. Following previous works, we take the particle radial mean free path to be spatially constant.
According to the classical Quasi-linear Theory (QLT) of particle scattering (Jokipii 1966), particle transport depends on both the level and the power spectrum of the magnetic field fluctuations. Turbulence in interplanetary space often has a Kolmogoroff form (q=5/3) in the inertial range (from 10-5 to 1 Hz). A 10 GV cosmic ray will resonate with meso-scale fluctuations in the frequency range between 10-6 and 10-5 Hz, where the spectrum is flatter with q=1 (Bieber et al. 1993). Thus the proton mean free path is taken to increase with rigidity following the standard model, such that λr = λ0(R/R0)(2-q), where λ0 is a free parameter, R0 = 2 GV, q = 1 for R > R0 and q = 5/3 for R < R0.
Analytical solutions of the focused transport equation are not known and numerical methods are applied to solve the focused transport equation. We use a Monte Carlo transport model (Agueda et al. 2008) to compute the proton intensities expected at 1 AU assuming that the solar source is static at two solar radii, the particle release is instantaneous and that particles are hypothetically moving at the speed of light. This Green's function of particle transport can be scaled to provide the Green's function for any other mono-energetic particles.
Cosmic ray transport in the geomagnetic field
The cosmic ray particles trajectories in the Earth's magnetic field are computed by numerical integration of backward trajectories in a model of the geomagnetic field (Smart et al. 2000). Thereby the effect is used that the path of a negatively charged particle with mass, m, charge, q, and speed, v, in a static magnetic field, B, is identical to that of a positively charged particle but with reverse sign of the velocity vector. Therefore, the common method to compute cosmic ray trajectories in the geomagnetic field is to calculate the trajectory in the reverse direction, i.e. the starting point of the reverse trajectory calculation is above the observation location in question at an altitude of typically 20 km asl.
Cosmic ray transport in the Earth’s atmosphere and detection by neutron monitors (NMs)
Primary cosmic ray particles that penetrate the atmosphere undergo multiple interactions resulting in showers of secondary particles. If the secondary nucleons (neutrons or protons) reach the ground, they can be detected by NMs.
The transport of cosmic ray particles through the Earth’s atmosphere and the detection of the nucleonic component of the secondary cosmic rays are combined in the so-called NM yield function. Thereby the NM yield function can directly be used to determine the cosmic ray flux at the top of the Earth’s atmosphere from the worldwide measurements of NMs.
Today, the yield functions of the NM are determined by simulating the interaction processes of the cosmic ray particles with the material in the atmosphere and with the material of the NM with Monte Carlo methods. In earlier days so-called latitude surveys, i.e. the NM count rate along a cruise over a large region of latitudes, were used to determine the yield functions.

 hesperia [dot] info [at] hesperia-space [dot] eu
hesperia [dot] info [at] hesperia-space [dot] eu